 |

|
Los datos hablan I#
#Si esta trabajando en Colab necesitarás instalar la Api de Makesens
#!pip install APIMakeSens
Graficando la Temperatura#
En este sección, realizaremos una visualización gráfica de los datos de temperatura obtenidos de las estaciones meteorológicas de la red RACIMO-Móncora para un periodo de tiempo determinado. Para esto, utilizaremos pricipalmente las librerias de Python MakeSens para acceder a los datos, Pandas para manejarlos y Matplotlib para visualizarlos.
# importamos las librerias que vamos a usar
import pandas as pd
import numpy as np
from MakeSens import MakeSens
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
Obtención de datos#
Mediante el uso de la API de MakeSens, descargamos los datos de temperatura de una de las estaciones (en este caso, usaremos los datos de la estación del Instituto Técnico Damazo Zapata) de la red de RACIMO-Móncora.
Para esto definimos:
la fechas de inicio y fin en formato:
%Y-%m-%d %H:%M:%SPor ejemplo:2023-08-01 00:00:00el ID de la estación
Frecuencia de muestreo:
1T,1H,D,W.
Frecuencias de muestreo:
Significado |
|
|---|---|
|
minutos |
|
horas |
|
días |
|
semanas |
ID de las Estaciones:
|
Colegio |
|---|---|
|
Instituto Técnico Damaso Zapata |
|
Colegio Santander |
|
Institución Educativa Nuestra Señora del Pilar |
|
Escuela Normal Superior |
|
Fundación Colegio UIS |
|
Institución Educativa Café Madrid |
|
Institución Educativa Piloto Simón Bolivar |
|
Institución Educativa Luis Carlos Galán Sarmiento |
|
Grupo Halley-UIS |
Luego, utilizamos la función download_data() con las variables definidas para obtener los datos de temperatura en un DataFrame de Pandas. Para más información sobre la API de MakeSens, puedes consultar la documentación.
#Definimos las fechas de inicio y fin de la descarga de datos (hemos elegido la última semana de abril)
fecha_inicio = "2023-04-23 00:00:00"
fecha_fin = "2023-04-30 00:00:00"
estacion = "mE1_00004" #Damaso Zapata
frecuencia = "1H"
#Descargamos los datos de MakeSens
data = MakeSens.download_data(estacion, fecha_inicio, fecha_fin, frecuencia)
Manejo de datos#
Una vez que descargamos el DataFrame con todos los datos de la estación, seleccionaremos los datos de temperatura en las columnas “temperatura” y “temperatura2” y los almacenaremos en un nuevo DataFrame: temp
¿Por qué tenemos dos columnas de temperatura?
Luego, renombraremos las columnas para que tengan nombres más cortos y entendibles. Finalmente, convertiremos el índice de los datos a formato de fecha y hora con la función to_datetime() para manejarlos facilmente y utilizarlos en la visualización.
Nota: Copiamos dataset
Debemos copiar el dataset para evitar errores de sincronización de datos con el dataset viejo.
#Obtenemos los datos de temperatura de los sensores mediante una copia del dataFrame
temp = data[["ts","temperatura", "temperatura2"]].copy()
temp.columns = ["ts","T1", "T2"] #renombramos las columnas
temp = temp.set_index('ts')
temp.index = temp.index.strftime('%Y-%m-%d %H:%M:%S')
temp.index = pd.to_datetime(temp.index) #Convertimos el indice a formato fecha
temp.head() #exploremos como quedo nuestro nuevo dataFrame.
| T1 | T2 | |
|---|---|---|
| ts | ||
| 2023-04-23 00:00:00 | 25.461412 | 26.223011 |
| 2023-04-23 01:00:00 | 25.296955 | 26.060955 |
| 2023-04-23 02:00:00 | 25.188348 | 25.949191 |
| 2023-04-23 03:00:00 | 25.073048 | 25.849771 |
| 2023-04-23 04:00:00 | 25.000205 | 25.777762 |
Convertir los indices en formato de fecha, nos permite hacer cosas interesantes. Por ejemplo:
# Datos de un mes especifico
temp.loc['2023-04']
# Datos de un día especifico ?
| T1 | T2 | |
|---|---|---|
| ts | ||
| 2023-04-23 00:00:00 | 25.461412 | 26.223011 |
| 2023-04-23 01:00:00 | 25.296955 | 26.060955 |
| 2023-04-23 02:00:00 | 25.188348 | 25.949191 |
| 2023-04-23 03:00:00 | 25.073048 | 25.849771 |
| 2023-04-23 04:00:00 | 25.000205 | 25.777762 |
| ... | ... | ... |
| 2023-04-29 19:00:00 | 27.274842 | 27.945907 |
| 2023-04-29 20:00:00 | 27.512799 | 28.181474 |
| 2023-04-29 21:00:00 | 27.880514 | 28.550688 |
| 2023-04-29 22:00:00 | 27.937186 | 28.646966 |
| 2023-04-29 23:00:00 | 27.612088 | 28.328476 |
169 rows × 2 columns
Analisis de datos#
Para empezar a procesar los datos, primero debemos preguntarnos qué queremos analizar.
Primero vamos a determinar si los dos sensores miden la misma temperatura. Una manera de hacerlo es calculando el promedio entre las medida de los dos sensores de temperatura para obtener un único valor de temperatura por cada medición. Para esto, utilizaremos la función .mean() de Pandas.
#Calculamos la media de los datos de temperatura
temp_mean = temp.mean(axis=1) #¿Qué sucede si no agregamos la opción axis?
Ahora, utilizaremos la función .resample() de Pandas para agrupar los datos por día y obtener un único valor de temperatura por día mediante la media aritmética de los datos. Esto nos permitirá visualizar los datos de temperatura de forma más clara con un dato para cada día, el cual será más o menos representativo dependiendo del fenómeno que queramos analizar.
Por ejemplo, si queremos ver la tendencia de una semana, un mes o un año, un promedio diario sería más útil, pero si queremos ver la tendencia de un día, ya no sería tan útil.
Para más información sobre la función .resample(), consultar la documentación.
#Resampleamos los datos a 1 dia
temp_mean_d = temp_mean.resample("D").mean()
Visualización de datos#
Comenzamos creando una figura y un conjunto de ejes con la función subplots de Matplotlibs, y luego establecemos el estilo de la gráfica, en este caso “default” (por defecto). A continuación, graficamos diferentes series de datos de temperatura, incluyendo la temperatura promedio por hora, por día y la temperatura registrada por cada sensor. Además, rellenamos el área entre los dos sensores de datos.
Realizamos un formateo del eje de fechas para mostrar las etiquetas principales diariamente y las etiquetas menores cada 6 horas, esto con las funciones major_formatter, major_locator y minor_locator. Ajustamos los parámetros visuales de las marcas de los ejes para mejorar su apariencia mediante la función tick_params.
Finalmente, agregamos etiquetas y títulos a los ejes, mostramos una cuadrícula de fondo y añadimos una leyenda para identificar cada serie de datos. Luego, mostramos la gráfica resultante.
Revisa el modulo de Visualización de Datos para una introducción básica sobre matplotlib
#Generamos la figura
fig, ax = plt.subplots(figsize=(15, 5))
plt.style.use("default")
#Graficamos los datos
ax.plot(temp_mean, "--", label="Temperatura promedio", markersize=4, color="red", alpha=0.7)
ax.plot(temp_mean_d, "o-", label="Temperatura promedio por día", markersize=5, linewidth=2, color="orange")
ax.fill_between(temp_mean.index, y1 = temp.T1, y2 = temp.T2, alpha=0.3)
ax.plot(temp.T1, "-", label="Temperatura 1", alpha=0.5, color="green")
ax.plot(temp.T2, "-", label="Temperatura 2", alpha=0.5, color="blue")
#Formateamos el eje de fechas para que se vea mejor
ax.xaxis.set_major_formatter(mdates.DateFormatter('%b/%d'))
ax.xaxis.set_major_locator(mdates.DayLocator())
ax.xaxis.set_minor_locator(mdates.HourLocator(byhour=range(0,24,6)))
ax.tick_params(which='major', pad=15, length=8, labelsize=12, direction="inout", width=1.5)
ax.tick_params(which='minor', length=4)
#Agregamos la leyenda y los titulos
ax.set_ylabel("Temperatura [°C]", fontsize=15)
ax.set_title("Temperatura en el Dámaso Zapata, última semana de abril", fontsize=20)
ax.grid(alpha=0.3)
ax.legend(fontsize=12)
plt.show()
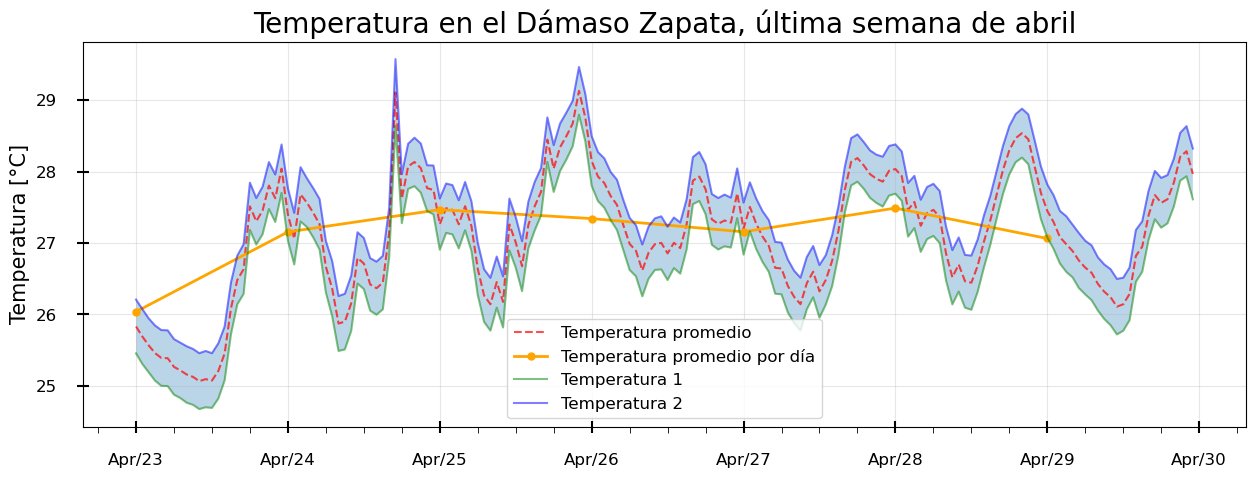
¿Los sensores miden la misma temperatura?
¿Cómo obtendrias la diferencia de temperatura entre los dos sensores?
¿Podrias usar esta diferencia para evaluar el comportamiento de los sensores?
¿Exite un ciclo diurno en la temperatura?#
En los datos podemos buscar comportamientos que varien durante periodos de tiempo determinado. Por ejemplo, podemos promediar el valor de la temperatura en todas las horas del dia buscando patrones. Para esto usamos a función .groupby() de Pandas.
Para más información sobre la función groupby, consultar la documentación.
# Primero agregamos una columna con el promedio de los sensores al DataFrame temp
temp['T_mean'] = temp_mean
# Segundo agregamos una columna "hora" al DataFrame temp que contenga la hora de cada dato
temp['hora'] = temp.index.hour.values
# Mostramos los primeros 5 datos del DataFrame
temp.head()
| T1 | T2 | T_mean | hora | |
|---|---|---|---|---|
| 2023-04-23 00:00:00 | 25.454298 | 26.207681 | 25.830989 | 0 |
| 2023-04-23 01:00:00 | 25.305798 | 26.074235 | 25.690016 | 1 |
| 2023-04-23 02:00:00 | 25.187994 | 25.943823 | 25.565909 | 2 |
| 2023-04-23 03:00:00 | 25.072544 | 25.844376 | 25.458460 | 3 |
| 2023-04-23 04:00:00 | 24.998870 | 25.780380 | 25.389625 | 4 |
Empleamos la función .groupby() para agrupar los datos por hora del día y obtener un único valor de temperatura por hora mediante la media aritmética de los datos. Esto nos permitirá visualizar los datos de temperatura de forma más clara con un dato para cada hora del día, el cual será más o menos representativo dependiendo del fenómeno que queramos analizar. Además de obtener el promedio de la temperatura para cada hora, también podemos obtener los valor máximos y mínimos registrados durante el periodo de tiempo analizado, esto con las funciones .max() y .min() de Pandas, respectivamente.
# Agrupamos los valores de la temperatura por hora y promediamos para el promedio
horario = temp['T_mean'].groupby(temp['hora']).mean()
horario_1 = temp['T1'].groupby(temp['hora']).mean()
# horario_2 = temp['T2'].groupby(temp['hora']).mean()
#También podemos obtener los valores máximos y minimos de temperatura durante la semana para cada hora del promedio
horario_max = temp['T_mean'].groupby(temp['hora']).max()
horario_min = temp['T_mean'].groupby(temp['hora']).min()
Una vez obtenidos los valores promedio de temperatura por hora, graficamos el promedio, el máximo y el mínimo de cada hora de la misma forma que en el proceso anterior.
#Generamos la figura y utilizamos el estilo por defecto
fig, ax = plt.subplots(figsize=(10, 5))
plt.style.use("default")
#Graficamos los datos
ax.plot(horario_max, label="Temperatura máxima", alpha=0.6, linestyle='--',color="red")
ax.plot(horario, label="Temperatura por hora", alpha=0.6, linestyle='-',color="green")
ax.plot(horario_min, label="Temperatura mínima", alpha=0.6, linestyle='--',color="blue")
#Coloreamos el area entre las lineas de maximo y minimo
ax.fill_between(horario_max.index, horario_max, horario_min, alpha=0.3, color="yellow")
#Formateamos el eje de fechas para que se vea mejor
ax.tick_params(which='major', pad=10, length=8, labelsize=12, direction="inout", width=1.5)
ax.tick_params(which='minor', length=4)
ax.set_xticks(range(0,24,5))
ax.set_xticks(range(0,24,1), minor=True)
ax.set_xticklabels(["00:00", "05:00", "10:00", "15:00", "20:00"], fontsize=12)
#Agregamos la leyenda, los titulos y la grilla
ax.set_ylabel("Temperatura [°C]", fontsize=15)
ax.set_xlabel("Hora", fontsize=15)
ax.set_title("Ciclo de temperatura diario para una semana de datos", fontsize=18)
ax.grid(alpha=0.3)
ax.legend(fontsize=12)
#Mostramos la figura
plt.show()
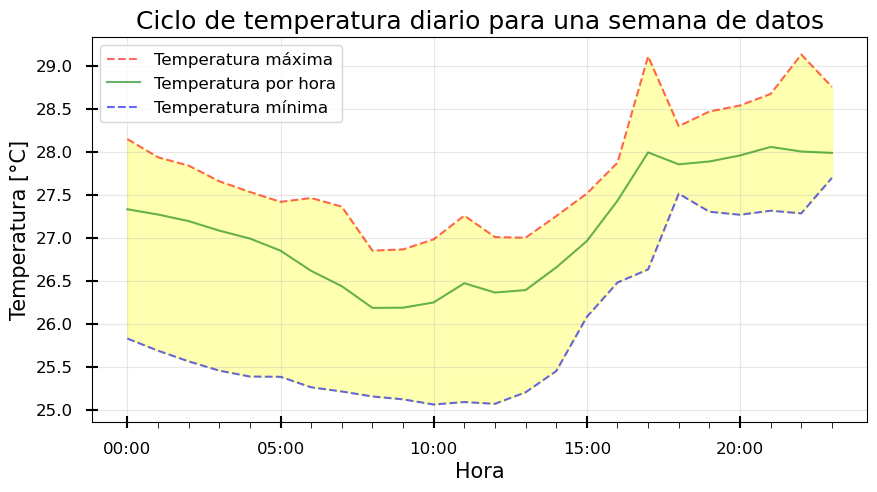
¿Este ciclo tiene sentido para ti?
¿Cómo piensas que se modificaria la grafica si ampliamos el periodo de los datos?
Cuartiles y Digrama de Caja y Bigotes#
A primera vista, podemos observar que el área sombreada entre los valores máximos y mínimos registrados por hora es amplia, lo que nos indica que la temperatura varía durante los días, dependiendo de la epoca del año. Por esto, vale la pena pensar:
¿Qué tan representativo es el promedio de cada hora respecto al comportamiento real?
En este caso, con representativo nos referimos a que tan cercano es el promedio de cada hora a la temperatura real registrada durante ese periodo de tiempo. Para responder esta pregunta podemos tener una visión más clara si calculamos los cuartiles del conjunto de datos.
Con esto en mente, definiremos las funciones que nos permitirán calcular los cuartiles de los datos. Para esto, utilizaremos las funciones .quantile() y .median() de numpy. Luego, estas funciones serán aplicadas a los datos agrupados por hora para obtener los cuartiles de cada hora, esto mediante la función .agg() de Pandas.
# Definimos las funciones para cada cuartil
def q1(x):
return x.quantile(0.25)
def q2(x):
return x.median()
def q3(x):
return x.quantile(0.75)
# Agrupamos los valores de la temperatura por hora y calculamos los cuartiles y el promedio
cuartiles = temp['T_mean'].groupby(temp['hora']).agg([q1, q2, q3, np.mean])
Una vez obtenidos los cuartiles de los datos, los graficaremos junto al promedio, los máximos y los mínimos de los datos.
# Generamos la figura
fig, ax = plt.subplots(figsize=(10, 5))
# Graficamos los datos a partir del DataFrame con la función plot de pandas
cuartiles.plot(ax=ax, alpha=0.7, legend=False, style=["--","--","--","-"], color=["black","purple","blue","green"])
# Graficamos los valores máximos y mínimos
ax.plot(horario_max, label="Temperatura máxima", alpha=0.6, linestyle='--',color="red")
ax.plot(horario_min, label="Temperatura mínima", alpha=0.6, linestyle='--',color="blue")
# Coloreamos el area entre las lineas de maximo y minimo
ax.fill_between(horario_max.index, horario_max, horario_min, alpha=0.3, color="yellow")
# Formateamos el eje de fechas para que se vea mejor
ax.tick_params(which='major', pad=10, length=8, labelsize=12, direction="inout", width=1.5)
ax.tick_params(which='minor', length=4)
ax.set_xticks(range(0,24,5))
ax.set_xticks(range(0,24,1), minor=True)
ax.set_xticklabels(["00:00", "05:00", "10:00", "15:00", "20:00"], fontsize=12)
# Agregamos la leyenda, los titulos y la grilla
ax.set_ylabel("Temperatura [°C]", fontsize=15)
ax.set_xlabel("Hora", fontsize=15)
ax.set_title("Ciclo Temperatura Diario", fontsize=20)
ax.legend()
ax.grid(alpha=0.3)
# Mostramos la figura
plt.show()
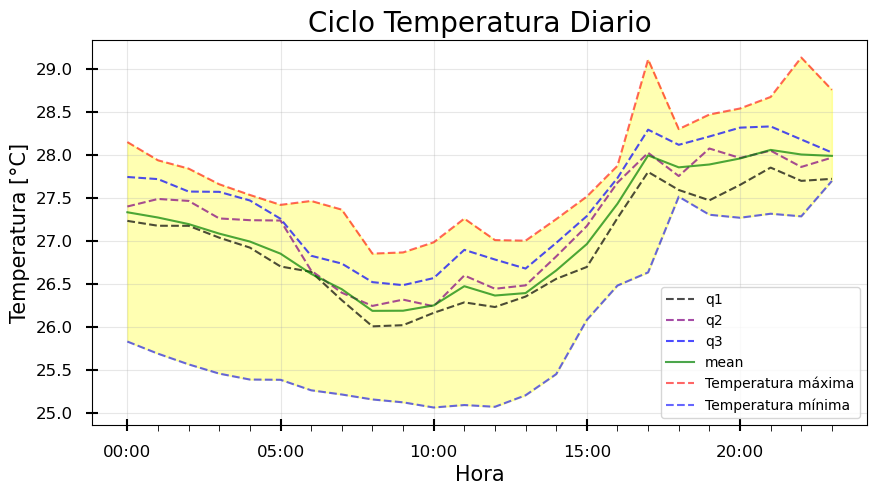
¿Qué puedes decir de los cuartiles de los datos respecto al promedio?
¿Qué puedes decir de los cuartiles de los datos respecto a los valores máximos y mínimos?
¿Qué dice esto de la representatividad del promedio de cada hora?
Puede que la visualización de los cuartiles, el promedio y los valores extremos de la forma anterior no sea la más adecuada para analizar los datos. Por esto, podemos graficar los cuartiles, el promedio y los valores extremos de una forma más clara utilizando un gráfico de cajas y bigotes. Para esto, emplearemos la librería Seaborn, la cual es una librería de visualización estadística de datos basada en Matplotlib.
En la figura podemos obserbar un ejemplo de un gráfico de cajas y bigotes. En este gráfico, la caja representa el rango intercuartil (IQR), la línea horizontal dentro de la caja representa la mediana (Q2), los bigotes representan los valores máximos y mínimos, y los puntos representan los valores atípicos. Estos valores máximos y mínimos se calculan como 1.5 veces el rango intercuartil (IQR) por encima del tercer cuartil (Q3) y por debajo del primer cuartil (Q1), respectivamente, lo cual es diferente a los valores máximos y mínimos calculados anteriormente, por tanto, los valores atípicos son aquellos por fuera de estos límites. El uso de este gráfico nos permite visualizar de forma más clara el conjunto de los datos y los valores atípicos.

Con esto en mente, importamos la librería Seaborn y, con ayuda de la función .boxplot() de Seaborn, realizaremos un gráfico de cajas y bigotes para los datos agrupados por hora. Además, graficaremos los valores máximos, mínimos y el promedio de los datos, para ver su relación con la gráfica de cajas y bigotes.
# Importamos la libreria seaborn
import seaborn as sns
# Generamos la figura
fig, ax = plt.subplots(figsize=(10, 5))
# Graficamos los datos a partir del DataFrame con la función boxplot de seaborn
sns.boxplot(data = temp, x='hora', y='T_mean', ax=ax)
# Graficamos el promedio
ax.plot(horario, "o-", label="Temperatura promedio", alpha=0.6,color="black")
# Graficamos los valores máximos y mínimos
ax.plot(horario_max, label="Temperatura máxima", alpha=0.6, linestyle='--',color="red")
ax.plot(horario_min, label="Temperatura mínima", alpha=0.6, linestyle='--',color="blue")
# Formateamos el eje de fechas para que se vea mejor
ax.tick_params(which='major', pad=10, length=8, labelsize=12, direction="inout", width=1.5)
ax.tick_params(which='minor', length=4)
ax.set_xticks(range(0,24,5))
ax.set_xticks(range(0,24,1), minor=True)
ax.set_xticklabels(["00:00", "05:00", "10:00", "15:00", "20:00"], fontsize=12)
# Agregamos la leyenda, los titulos y la grilla
ax.set_ylabel("Temperatura [°C]", fontsize=15)
ax.set_xlabel("Hora", fontsize=15)
ax.set_title("Gráfica de cajas y bigotes para la temperatura por hora", fontsize=18)
ax.legend()
ax.grid(alpha=0.3)
# Mostramos la figura
plt.show()
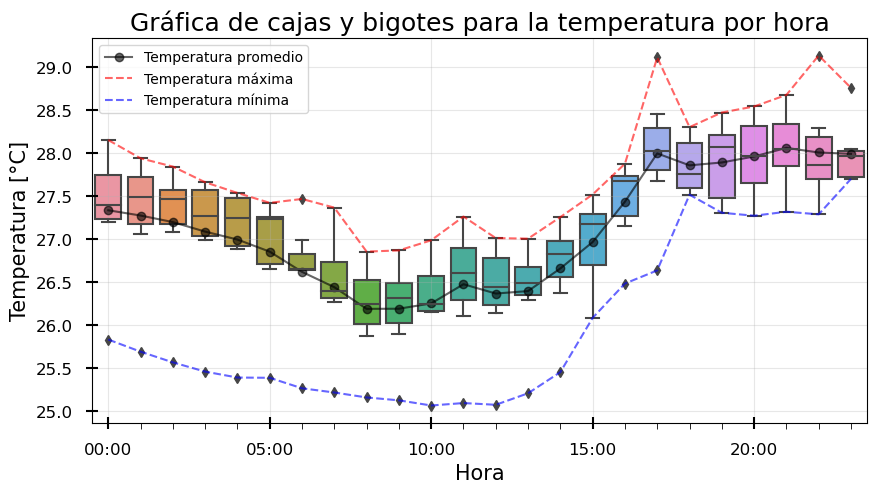
¿Qué puedes decir de los valores atípicos?
¿Cómo se relacionan los valores atípicos con los valores máximos y mínimos?
¿Puedes decir que tan representativo es el promedio de cada hora respecto a los datos reales?